Differential Flatness

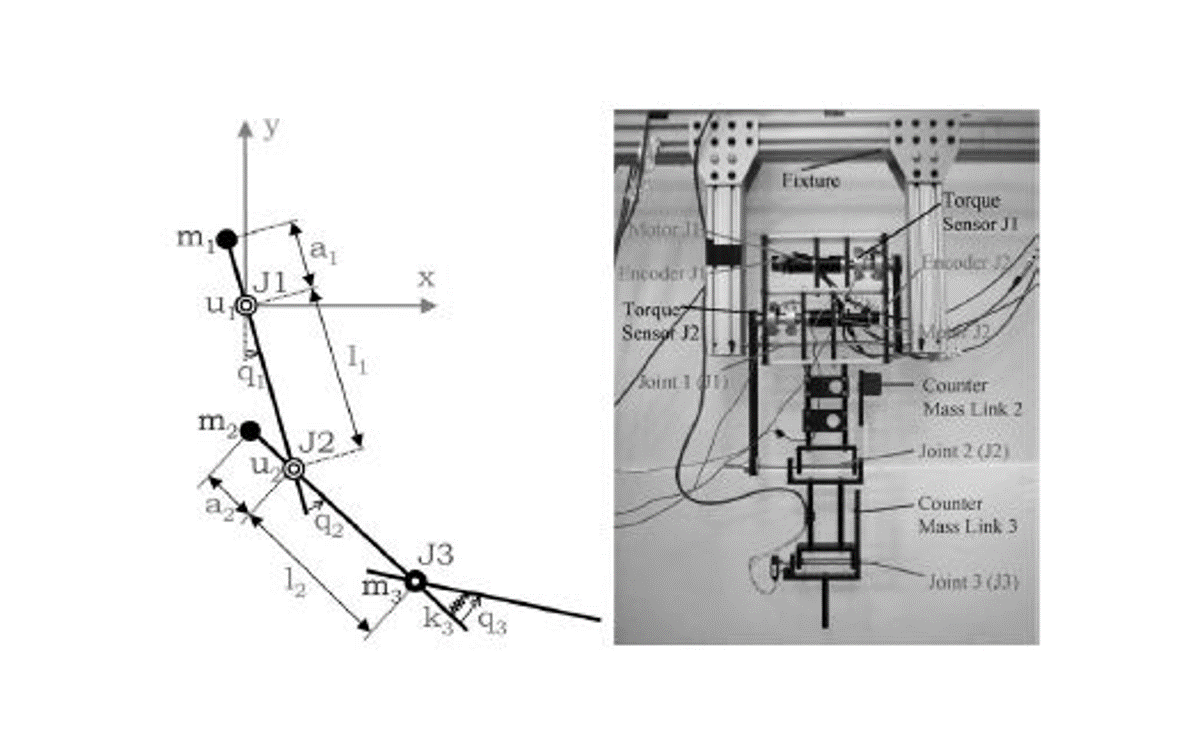
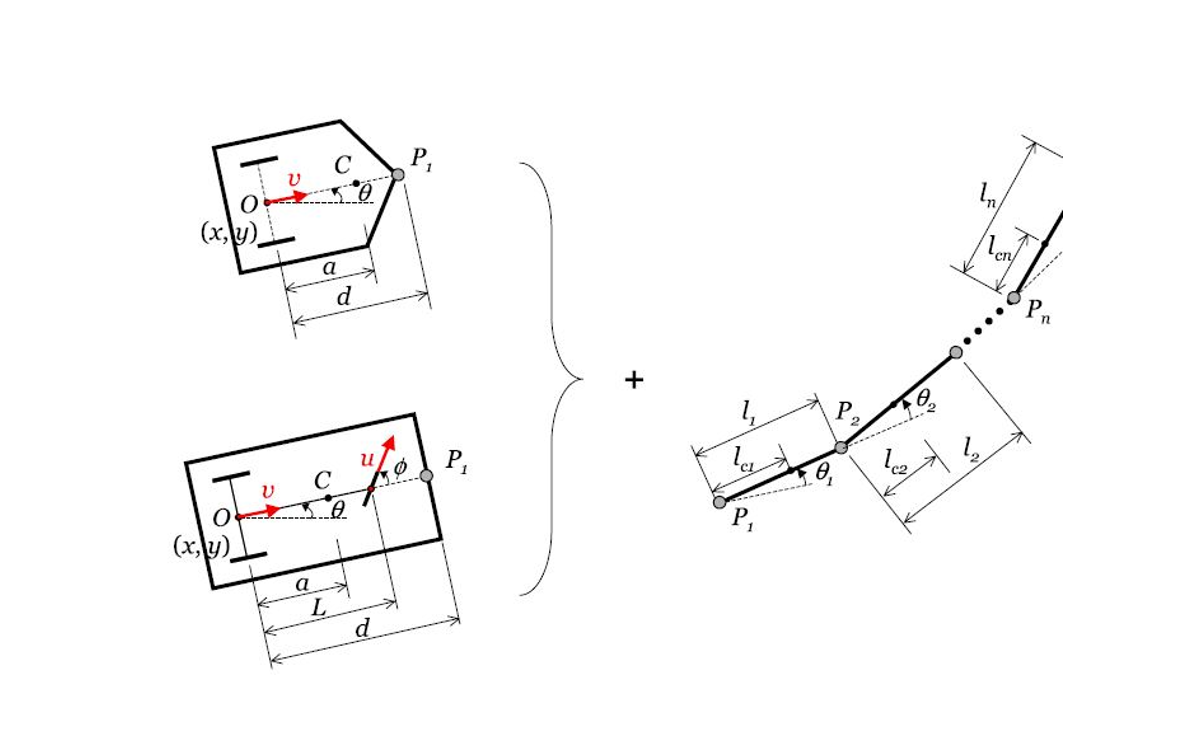
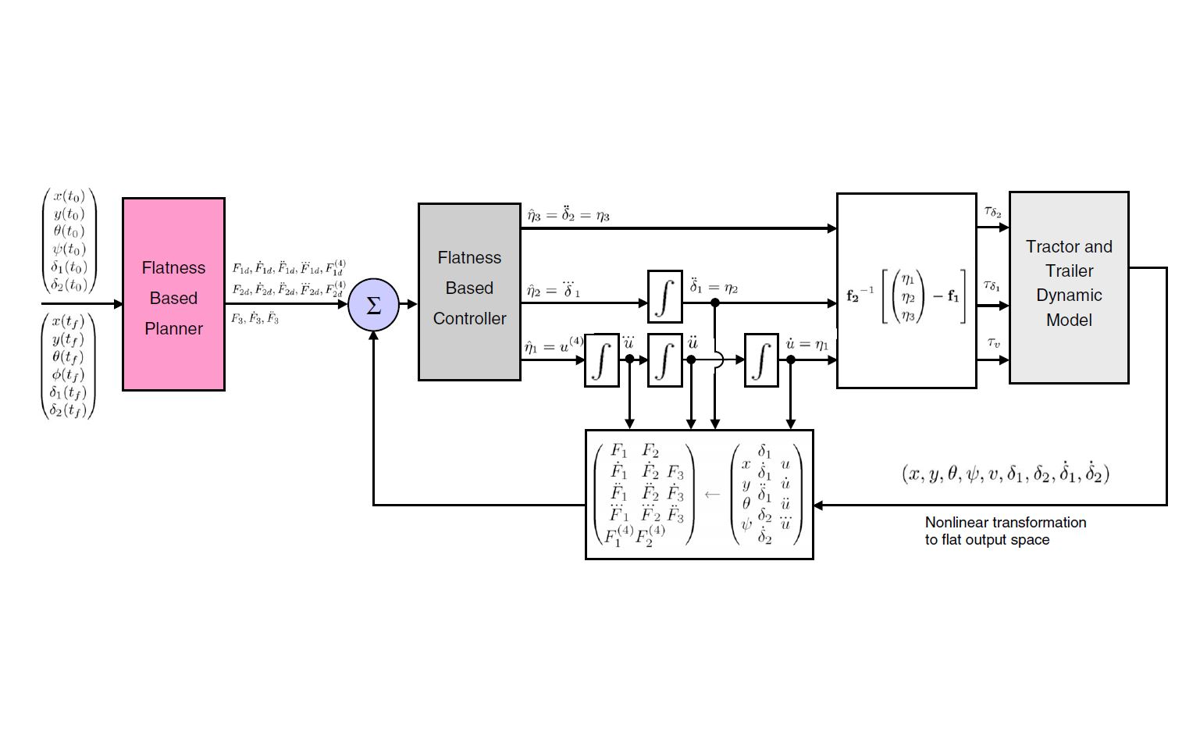
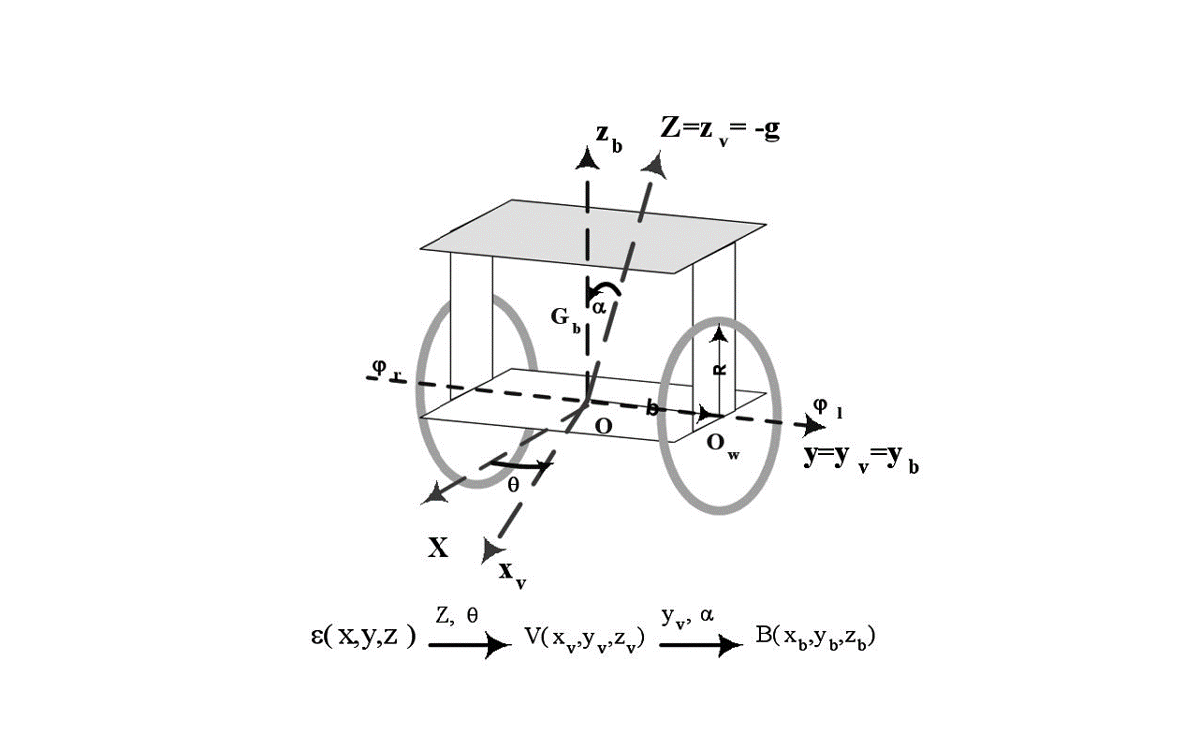
Classes of nonlinear dynamic systems can be transformed to linear and controllable forms using static and dynamic feedback.  These structures often arise in dynamic equations of open and closed-chain robots, mobile vehicles, and chemical reactors. In some cases, the dynamic equations of a system may not naturally be in a differentially flat form. However, one can redesign a system through geometry and inertia distribution to make it in a differentially flat form. These techniques have been demonstrated for  number of different systems, including design of manipulator arms and mobile vehicles.

For differentially flat systems, the planning and control problems can be solved effectively using the linear and controllable forms. These methods have applications in the control of under-actuated robots, nonholonomic robots, and space robots.

Sometimes, through modulation of geometric and inertial properties, a system can be designed to be differentially flat. These methods are demonstrated using examples of under-actuated open and closed chain robots.